Le jeu de la vie de Conway
Le jeu de la vie de Conway est un automate cellulaire conçu par le mathématicien britannique John Horton Conway en 1970. Il s'agit d'un jeu sans joueur, ce qui signifie que son évolution est déterminée par son état initial, ne nécessitant aucune intervention supplémentaire. On interagit avec le jeu de la vie en créant une configuration initiale et en observant son évolution. Dans ce projet, j'ai décidé de tester différentes densités et de voir lesquelles survivraient le plus longtemps. Dans le cadre d'une deuxième partie du projet, j'ai décidé d'étendre cela à une version hexagonale du jeu et de voir les taux de survie dans ce nouvel environnement.
Voici un petit environnement que j'ai construit pour jouer au jeu avec le fameux planeur déjà dessiné.
Lors de la conception du jeu, j'ai décidé de faire en sorte que le plateau se comporte comme un tore. Cela signifie que la planche s'enroule sur elle-même, de sorte que la rangée du haut soit connectée à la rangée du bas et que la droite soit connectée à la gauche. Cela permet au jeu d'avoir un plateau apparemment « infini » même s'il est en réalité assez petit. Ceci est utile car dans un monde idéal, nous voudrions tester les densités sur une carte infinie.
Résultats sur une grille quadrillé
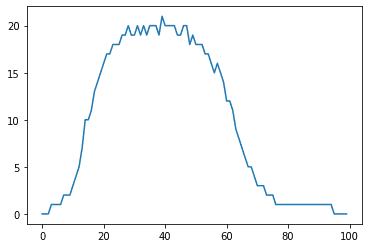
Comme nous pouvons le constater, les densités qui offrent la plus grande capacité de survie se situent entre 25 % et 50 %. Je sais que les axes du graphique ne sont pas correctement nommés. Ce projet a été réalisé au cégep et pour obtenir le même graphique, il faudrait encore 10 heures de computations. Donc je m'excuse pour cela.
Le passage d'une grille carrée à une grille hexagonale
La partie difficile de cette nouvelle implémentation du jeu était de décider comment représenter le plateau en interne et faire en sorte que le jeu se déroule. J'aurais pu utiliser un système d'objets où chaque arête serait voisine mais j'ai décidé de rendre l'implémentation plus efficace. J'ai trouvé un moyen assez simple de représenter la grille hexagonale dans une matrice normale.


En utilisant la puissance de ces matrices, j'ai à nouveau simulé !

Comme nous pouvons le constater, les densités qui survivent le plus sont toujours autour de 25 à 50%. Ce qui est intéressant ici, c'est à quel point le graphique est « plus large ». Ainsi, en général, sur une grille hexagonale, tout motif a plus de chances de survivre plus longtemps qu'un motif tout aussi dense sur un plateau carré. Pour terminer, encore une fois, les axes ne sont pas nommés correctement.